Double Angle Identities How to Know Which Cos to Use

Substitution for a single variable Introduction. We use the cosine double angle identity again with.

Double Angle Identities Free Math Help Trigonometry Help Word Problem Worksheets

The less important identities.

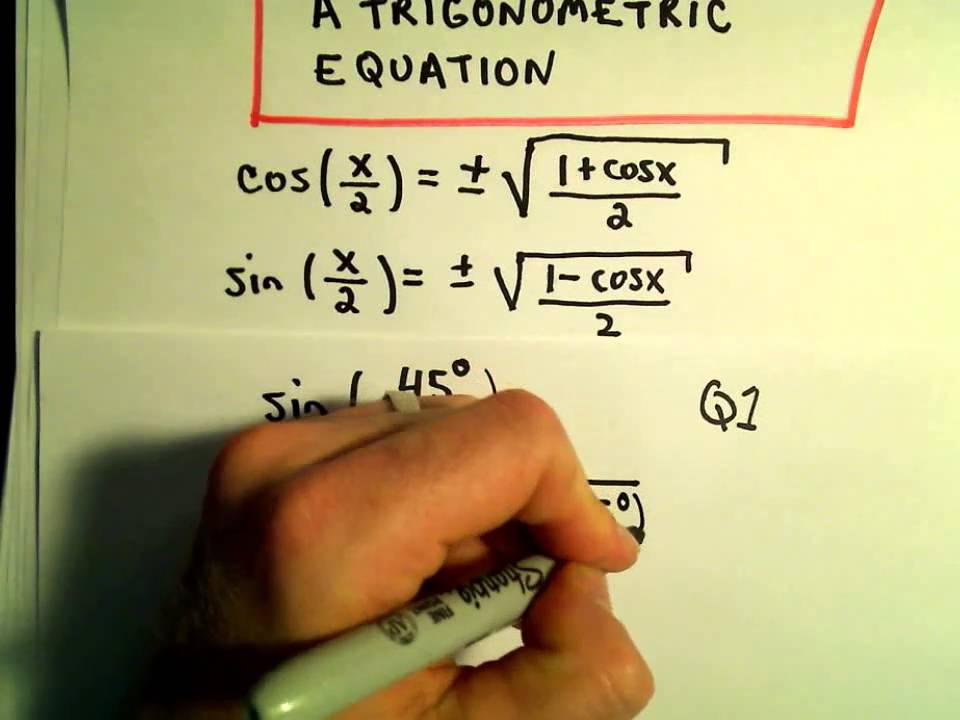
. Here is the proof of the sum formulas. We will undertake a full discussion of the assumptions system later but for now all we need to know are the following. You should know that there are these identities but they are not as important as those mentioned above.

Since these identities are proved directly from geometry the student is not normally required to master the proof. We can use the Pythagorean Identity to find the cosine of an angle if we know the sine or vice versa. List of trigonometric identities 2 Trigonometric functions The primary trigonometric functions are the sine and cosine of an angle.

From the exercise above we see that the compound angle identities can in fact be derived using a radius of any length. However all the identities that follow are based on these sum and difference formulas. Lets apply the Double Angle Identity for cosine.

However because the equation yields two solutions we need additional knowledge of the angle to choose the solution with the correct sign. The student should definitely know them. These are sometimes abbreviated sinθ andcosθ respectively where θ is the angle but the parentheses around the angle are often omitted eg sin θ andcos θ.

Earlier in this chapter we derived the compound angle identities using a unit circle radius text1 unit because it simplified the calculations. You only need to know one but be able to derive the other two from the Pythagorean formula. Before stating the result rigorously consider a simple case using indefinite integrals.

This last expression is an identity and identities are one of the topics we will study in this chapter. This procedure is frequently used but not all integrals are of a form that permits its use. Functions consisting of powers of the sine and cosine can be integrated by using substitution and trigonometric identities.

Double angle formulas for sine and cosine. Set This means or in differential form Now where is an arbitrary constant of integration. Both m and.

We know that cosine squared of two x is going to be equal to 12 times one plus cosine of double this angle so cosine of four x. Note that there are three forms for the double angle formula for cosine. In order to make SymPy perform simplifications involving identities that are only true under certain assumptions we need to put assumptions on our Symbols.

Fairly straightforward to take the indefinite integral or to take the antiderivative of these two pieces. Use cos2x1-sin2x1-u2 to replace the leftover cosines. If we know the quadrant where the angle is we can easily choose the correct solution.

Once again Ive got an even exponent. The tangent tan of an angle is the ratio of the sine to the cosine. These can sometimes be tedious but the technique is straightforward.

Cos2 x 1 4 sin x 1 2 sin x y cos2 x and y 1 sin4 x 1 sin2 x 795 Trigonometric Identities and Equations IC 6 c i-1 1 x y CHAPTER OUTLINE 111 Introduction to Identities 112 Proving Identities 113 Sum and Difference Formulas 114 Double. But what do I do here.

This Page Gives The Double Angle Formulas And Half Angle Formula And Explains What They Are Used For Doub Writing Linear Equations Trigonometry Math Formulas

Youtube Trigonometry Evaluation Expressions

Ch 5 5 Multiple Angle And Product To Sum Formulas Ppt Download Free Math Help Trigonometry Word Problem Worksheets